問5 下図の直列系の信頼性ブロック線図(図a)及び並列系の信頼性プロック線図(図b)がそれぞれ要素1及び2から構成されている。要素1、2は、それぞれ、定数故障率λ1、λ2をもち、時刻tにおける信頼度R1(t)、R2(t)をもつとき、信頼度又は故障率に関する(1)~(5)の記述のうち、適切でないものはどれか。
ただし、要素は系の運用開始時刻0で新品同様、すなわちR1(0)=1、R2(0)=1であるものとし、また、要素の故障は、独立に起き、修理はないものとする。
 |
 |
|
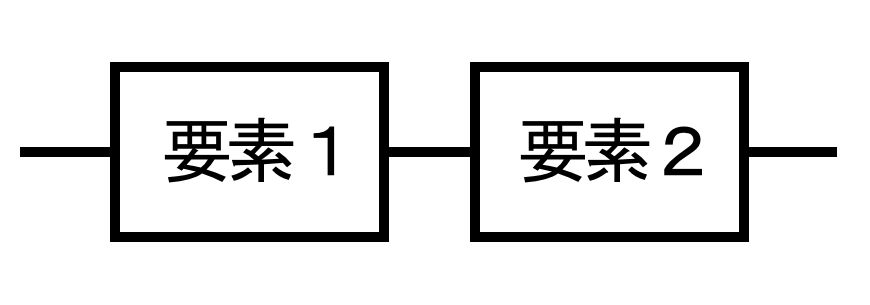
図a 直列系の信頼性ブロック線図 |
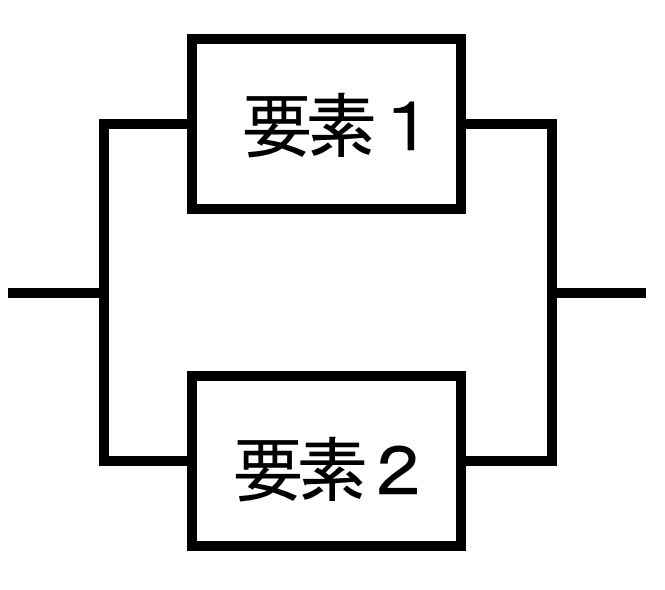
図b 並列系の信頼性ブロック線図 |
要素1の定数故障率 : λ1
要素1の信頼度 : R1(t)
要素2の定数故障率 : λ2
要素2の信頼度 : R2(t)
(1)時刻t での要素1 の信頼度R1(t)は、
R1(t) = exp(-λ1t)
となる。
(2)時刻t での直列系の信頼度RS(t)は、
RS(t) = R1(t)R2(t)
となる。
(3)時刻t での直列系の故障率λS(t)は、
λS(t) = λ1+λ2
となる。
(4)時刻t での並列系の信頼度Rp(t)は、
となる。
(5)時刻t での並列系の故障率 λp(t)は、
λp(t) = λ1λ2t
となる。

このページは、2014年の労働安全衛生コンサルタント試験の「産業安全一般」問題の解説と解答例を示しています。
解説文中の法令の名称等は、適宜、略語を用いています。また、引用している法令は、読みやすくするために漢数字を算用数字に変更するなどの修正を行い、フリガナ、傍点等は削除しました。
他の問題の解説をご覧になる場合は、グローバルナビの「安全衛生試験の支援」か「パンくずリスト」をご利用ください。
柳川に著作権があることにご留意ください。
| 2014年度(平成26年度) | 問05 | 難易度 | 信頼性ブロック線図の問題は基本を押さえておけば正答できる。必ず正答できるようにしておくこと。 |
|---|---|---|---|
| 信頼性ブロック線図 | 3 |
問5 下図の直列系の信頼性ブロック線図(図a)及び並列系の信頼性プロック線図(図b)がそれぞれ要素1及び2から構成されている。要素1、2は、それぞれ、定数故障率λ1、λ2をもち、時刻tにおける信頼度R1(t)、R2(t)をもつとき、信頼度又は故障率に関する(1)~(5)の記述のうち、適切でないものはどれか。
ただし、要素は系の運用開始時刻0で新品同様、すなわちR1(0)=1、R2(0)=1であるものとし、また、要素の故障は、独立に起き、修理はないものとする。
 |
 |
|
図a 直列系の信頼性ブロック線図 |
図b 並列系の信頼性ブロック線図 |
要素1の定数故障率 : λ1
要素1の信頼度 : R1(t)
要素2の定数故障率 : λ2
要素2の信頼度 : R2(t)
(1)時刻t での要素1 の信頼度R1(t)は、
R1(t) = exp(-λ1t)
となる。
(2)時刻t での直列系の信頼度RS(t)は、
RS(t) = R1(t)R2(t)
となる。
(3)時刻t での直列系の故障率λS(t)は、
λS(t) = λ1+λ2
となる。
(4)時刻t での並列系の信頼度Rp(t)は、
Rp(t) = 1-{1-R1(t)}{1-R2(t)}
となる。
(5)時刻t での並列系の故障率 λp(t)は、
λp(t) = λ1λ2t
となる。
正答(5)
【解説】
1 本問を解くための前提条件
問題文には書かれていないが、当然の前提として、本問では要素1と要素2の故障は互いに独立に発生するとされている。
また、図bの並列系は、どちらかが正常であれば、全体として正常に作動するとされているようだ。ただ、これが問題文に書かれていないことにはやや疑問を感じる。
なお、図aの直列系では、どちらか一方が故障すると系全体が使用できなくなることは当然である。
2 信頼度と故障率
信頼度R(t)とは、時刻tにおいて系が正常に動作している確率である。具体的な数字を例に挙げると、サンプルが100個あり、時刻tでそのうち80個が正常に動作しているとすると、時刻tの信頼度は0.8である。すなわち最初のサンプル数がNで時刻tにおいてS(t)個のサンプルが正常に動作しているとすると、
である。両辺を時間で微分して、整理すると、
となる。ただし、F(t)は、時刻tまでに故障したサンプル数である。
一方、故障率λとは、時刻tにおいて正常に動作しているサンプルに対する、あらたに故障するものの割合である。時刻tで80個のサンプルのうち8個が故障したとすると、時刻tの故障率は0.1となる。つまり、
となる。ただし、本問では故障率λはtによらず一定であるとされている。
3 並列回路と直列回路
1で示したことを前提とすれば、要素1と要素2が直列につながっている図aでは、全体の信頼度RSは、どちらか一方が故障すると系全体が使用できなくなるので、
RS=R1 × R2
となり、並列に繋がっている図bでは、どちらか一方が故障していなければ、系は正常に作動するので、
Rp=1-(1-R1)×(1-R2)
となる。複雑な系であってもこれらの組合せで全体の信頼度を算出できる。
一方、故障率は、これらが互いに独立だとすると、これが直列につながっていれば全体の故障率λSは、
λS=1-(1-λ1)×(1-λ2)
となる。整理すると、
λS=λ1+λ2+λ1λ2
となるが、λ≒0であり、高次の項(λ1λ2)は無視することができるので、
λS=λ1+λ2
としてよい。一方、並列につながっている図bでは、
λS=λ1 × λ2
となる。ここまでは、理解しておかなければならない。その上で、本問を解いてみよう。
(1)適切である。この種の問題は、実際に数字を当てはめると分かりやすい。λが時刻tによらないので故障率を0.1とすると、t=1のとき、この系は90%の確率で正常に動作している。t=2のときは、90%のさらに1割が故障するから、正常に動作するのは、0.9×0.9すなわち81%となる。t=3のときは、0.9×0.9×0.9すなわち、72.9%となる。これで分かると思うが、指数関数になっているのである。
その上で、上記の解説から、2の最後に示した式の両辺を積分すると、
である。すなわち、本問に当てはめると、
R1(t) = exp(-λ1t)
となる。この式は公式として覚えておいた方が良い。
(2)適切である。上記解説で示した通り。直列系では、片方でも故障すれば全体が使用できなくなるので、
RS(t) = R1(t)R2(t)
となる。
(3)適切である。上記解説で示した通り、
λS(t) = λ1+λ2
となる。高次の項を無視しているので、これを正答とした受験生もいるようだが、(5)の方が明らかにおかしいことが分からなければならない。
(4)適切である。上記解説で示した通り。並列系では、一方が正常であれば系全体が正常に作動するので、
Rp(t) = 1-{1-R1(t)}{1-R2(t)}
となる。
(5)適切ではない。上記解説で示した通りである。正しくは、
λp(t) = λ1λ2
である。そもそもλはtによらず一定であるから、並列にしたからと言って、tの関数になるわけがないのである。しかも、本肢の通りだとすると、tが極めて大きくなると、故障率が1を超えてしまう。こんなことはあり得ない。
実を言えば、本問は考えるまでもなく、これがおかしいと気付くことができる問題なのである。








